Cryptography in Bitcoin
Bitcoin relies on several cryptographic primitives to secure transactions, prove ownership, and maintain the integrity of the blockchain. Understanding these cryptographic foundations is essential for grasping how Bitcoin achieves trustless security.
The Power of Cryptography
Cryptography enables remarkable capabilities that seem almost magical:
- Prove knowledge without revealing it: You can prove you know a secret (like a private key) without ever exposing the secret itself. This is how you sign Bitcoin transactions.
- Create unforgeable signatures: Only the holder of a private key can create a valid signature, but anyone can verify it with the corresponding public key.
- Commit to data irrevocably: Hash functions create unique fingerprints that bind you to specific data without revealing it until you choose to.
- Verify integrity instantly: Detect any tampering with data, no matter how large, by comparing small hash values.
These concepts aren't unique to Bitcoin. You encounter cryptography daily:
| Application | Cryptographic Use |
|---|---|
| HTTPS/TLS | Encrypts web traffic, verifies website identity |
| PGP/GPG | Email encryption and digital signatures |
| Signal/WhatsApp | End-to-end encrypted messaging |
| SSH | Secure remote server access |
| Password Storage | Hashing passwords so they're never stored in plain text |
Bitcoin combines these proven cryptographic techniques in a novel way to create a trustless monetary system.
Overview
Bitcoin uses cryptography for three main purposes:
- Ownership & Authentication: Proving you own bitcoin without revealing your private key
- Integrity: Ensuring data hasn't been tampered with
- Proof-of-Work: Securing the blockchain through computational work
Hash Functions
A cryptographic hash function takes any input data and produces a fixed-size output (the "hash" or "digest"). Hash functions are one-way: easy to compute, but practically impossible to reverse.
Properties of Cryptographic Hash Functions:
| Property | Description |
|---|---|
| Deterministic | Same input always produces same output |
| Fast | Quick to compute for any input |
| One-way | Cannot derive input from output |
| Collision-resistant | Infeasible to find two inputs with same output |
| Avalanche effect | Small input change = completely different output |
SHA-256
Bitcoin's primary hash function is SHA-256 (Secure Hash Algorithm, 256-bit).
Characteristics:
- Output: 256 bits (32 bytes, 64 hex characters)
- Designed by NSA, published in 2001
- No known practical attacks
Example:
Input: "Hello"
SHA-256: 185f8db32271fe25f561a6fc938b2e264306ec304eda518007d1764826381969
Input: "Hello!"
SHA-256: 334d016f755cd6dc58c53a86e183882f8ec14f52fb05345887c8a5edd42c87b7
Notice how adding a single character completely changes the output (avalanche effect).
Double SHA-256 (SHA256D)
Bitcoin often uses double SHA-256: SHA256(SHA256(data))
Used for:
- Block hashes
- Transaction IDs (TXIDs)
- Merkle tree nodes
- Proof-of-work
Why double hashing?
- Defense against length-extension attacks
- Additional security margin
- Historical design choice by Satoshi
Code: SHA-256 and Double SHA-256
RIPEMD-160 and Hash160
RIPEMD-160 produces a 160-bit (20-byte) hash, used in combination with SHA-256.
Hash160 = RIPEMD160(SHA256(data))
Used for:
- Bitcoin addresses (P2PKH, P2SH)
- Shorter than SHA-256, reducing address length
- Still cryptographically secure
Code: Hash160
Elliptic Curve Cryptography
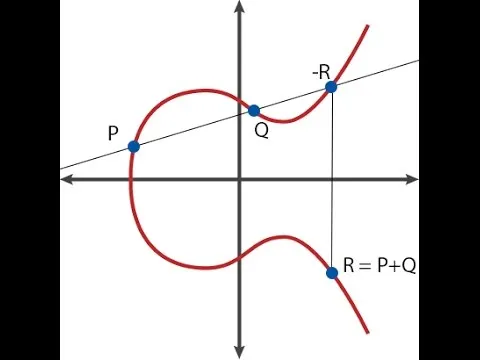
Elliptic Curve Cryptography (ECC) is a public-key cryptography system based on the algebraic structure of elliptic curves over finite fields.
Why Bitcoin uses ECC:
- Smaller key sizes than RSA (256-bit vs 3072-bit for equivalent security)
- Faster computation
- Lower bandwidth and storage requirements
The secp256k1 Curve
Bitcoin uses the secp256k1 elliptic curve (see ECDSA), defined by the equation:
y² = x³ + 7 (mod p)
Parameters:
- p (prime): 2²⁵⁶ - 2³² - 977
- Order (n): Number of points on the curve
- Generator point (G): Fixed starting point for key generation
Why secp256k1?
- Chosen by Satoshi (not the most common curve at the time)
- Efficiently computable
- No known weaknesses
- Parameters are "nothing up my sleeve" numbers (verifiably random)
Key Generation
Private Key:
- Random 256-bit number (1 to n-1)
- Must be kept secret
- Generated from cryptographically secure random source
Public Key:
- Derived from private key:
Public Key = Private Key × G - Point multiplication on the elliptic curve
- Cannot reverse to find private key (discrete logarithm problem)
- Can be shared publicly
Key Relationship:
Random Number → Private Key → Public Key → Bitcoin Address
(256 bits) (256 bits) (512 bits) (160 bits)
Code: Key Generation
The Discrete Logarithm Problem
Why can't you derive the private key from the public key?
Given Q = k × G where:
Qis the public key (known)Gis the generator point (known)kis the private key (unknown)
Finding k requires solving the Elliptic Curve Discrete Logarithm Problem (ECDLP), which is computationally infeasible for sufficiently large numbers.
Security Level:
- 256-bit private key = ~128 bits of security
- Would take billions of years with current technology
- Quantum computers could theoretically break this (see future considerations)
Digital Signatures
A digital signature proves:
- Authenticity: Message came from the claimed sender
- Integrity: Message hasn't been altered
- Non-repudiation: Sender cannot deny sending
ECDSA (Elliptic Curve Digital Signature Algorithm)
Bitcoin originally used ECDSA for all signatures.
Signing Process:
- Hash the message:
z = SHA256(message) - Generate random number
k(nonce) - Calculate point
R = k × G - Calculate signature:
s = k⁻¹(z + r × privateKey) mod n - Signature is the pair
(r, s)
Verification Process:
- Hash the message:
z = SHA256(message) - Calculate:
u1 = z × s⁻¹ mod n - Calculate:
u2 = r × s⁻¹ mod n - Calculate point:
P = u1 × G + u2 × PublicKey - Signature valid if
P.x = r
ECDSA Characteristics:
- Signature size: 70-72 bytes (DER encoded)
- Requires secure random nonce
k - Reusing
kexposes private key!
Code: ECDSA Signing and Verification
Schnorr Signatures
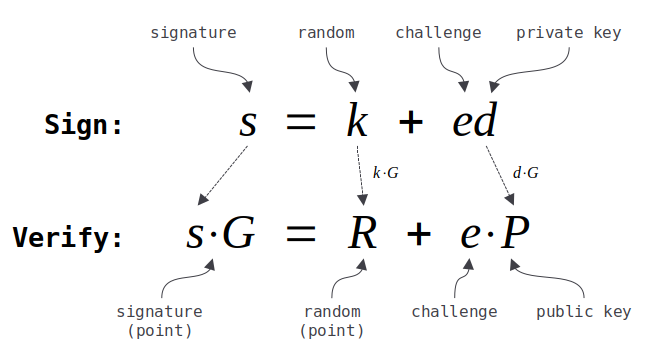
Schnorr signatures were introduced with the Taproot upgrade (2021).
Advantages over ECDSA:
- Simpler: Mathematically cleaner
- Smaller: Fixed 64-byte signatures
- Linearity: Enables key and signature aggregation
- Provably secure: Better security proofs
- Batch verification: Faster validation of multiple signatures
Signature Aggregation: Multiple signatures can be combined into one, enabling:
- MuSig: Multi-signature schemes that look like single signatures
- Privacy: Multi-party transactions appear as single-party
- Efficiency: Reduced transaction size and fees
Code: BIP-340 Schnorr Tagged Hash
Signing a Bitcoin Transaction
When you spend bitcoin:
- Construct transaction with inputs and outputs
- Create signature hash (sighash) of transaction data
- Sign the sighash with your private key
- Include signature in transaction's witness/scriptSig
- Broadcast transaction to network
- Nodes verify signature matches public key and transaction
Merkle Trees
A Merkle tree (or hash tree) is a data structure that efficiently summarizes and verifies large datasets.
Structure:
Merkle Root
/ \
Hash AB Hash CD
/ \ / \
Hash A Hash B Hash C Hash D
| | | |
Tx A Tx B Tx C Tx D
How Bitcoin Uses Merkle Trees
Block Structure:
- Each block contains a Merkle root in its header
- Merkle root summarizes all transactions in the block
- Changing any transaction changes the Merkle root
Benefits:
- Efficient verification: Prove transaction inclusion with O(log n) hashes
- Compact proofs: SPV nodes don't need full blockchain
- Data integrity: Any tampering is immediately detectable
Merkle Proofs (SPV)
Simplified Payment Verification allows lightweight clients to verify transactions without downloading the full blockchain.
To prove Tx B is in a block:
Provide: Hash A, Hash CD
Client calculates:
1. Hash B (from Tx B)
2. Hash AB = SHA256(Hash A + Hash B)
3. Merkle Root = SHA256(Hash AB + Hash CD)
4. Compare with block header's Merkle root
Code: Merkle Tree and Proof Verification
Address Encoding
Base58Check
Base58 encoding uses 58 characters (excluding 0, O, I, l to avoid confusion):
123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz
Base58Check adds a checksum:
- Add version byte prefix
- Calculate checksum:
SHA256(SHA256(data))(first 4 bytes) - Append checksum to data
- Encode in Base58
Used for: Legacy addresses (1..., 3...)
Bech32 and Bech32m
Bech32 encoding (BIP-173) is used for SegWit addresses:
Characteristics:
- Case-insensitive
- Better error detection (BCH codes)
- QR code friendly
- Prefix:
bc1for mainnet,tb1for testnet
Address Types:
Bech32m (BIP-350) is a modified version for Taproot addresses with improved error detection.
Code: Address Generation (Full Pipeline)
Cryptographic Security Assumptions
What Bitcoin Assumes
Bitcoin's security relies on these assumptions holding true:
| Assumption | If Broken |
|---|---|
| SHA-256 is collision-resistant | Could create invalid blocks |
| SHA-256 is preimage-resistant | Could forge proof-of-work |
| ECDLP is hard | Private keys could be derived from public keys |
| Random number generation is secure | Private keys could be predicted |
Quantum Computing Considerations
Potential Threats:
- Shor's algorithm could break ECDSA/Schnorr (public key → private key)
- Grover's algorithm could speed up SHA-256 attacks (but only quadratic speedup)
Current Status:
- No quantum computer capable of breaking Bitcoin exists today
- Estimates suggest decades before practical quantum threats
- Bitcoin community is researching post-quantum solutions
- Addresses that haven't revealed public keys are safer
Mitigations:
- Don't reuse addresses (limits public key exposure)
- Post-quantum signature schemes being researched
- Soft fork could add quantum-resistant signatures
Summary
| Cryptographic Primitive | Purpose in Bitcoin |
|---|---|
| SHA-256 | Block hashing, TXIDs, PoW |
| SHA-256d (double) | Block headers, Merkle trees |
| RIPEMD-160 | Address generation (Hash160) |
| secp256k1 (ECC) | Key pairs, signatures |
| ECDSA | Legacy transaction signatures |
| Schnorr | Taproot signatures, aggregation |
| Merkle Trees | Transaction summarization, SPV proofs |
| Base58Check | Legacy address encoding |
| Bech32/Bech32m | SegWit/Taproot address encoding |
Resources
- Bitcoin Developer Guide - Transactions - Official documentation on transaction signing
- Learn Me a Bitcoin - Visual explanations of Bitcoin cryptography
- BIP-340: Schnorr Signatures - Schnorr signature specification
- SEC 2: Recommended Elliptic Curve Domain Parameters - secp256k1 specification
- libsecp256k1 - Bitcoin Core's optimized secp256k1 C library
